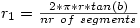Original math for Polar Grids
The angle of the polar grid is kept constant with the following theory.
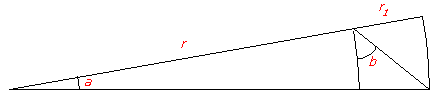
When a is small and r large, the small edge of the pie could be considered straight.
With b = 45 degrees, r1 equals the small pie edge.
The approximation above in math:
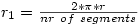
For the circle we get:
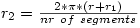
From the mathematical rule:
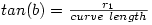
we can deduce: